3 What is Logic?

There’s an ancient view, still widely held, that what makes human beings special—what distinguishes us from the “beasts of the field”—is that we are rational. What does rationality consist in? That’s a vexed question, but one possible response goes roughly like this: we manifest our rationality by engaging in activities that involve reasoning—making claims and backing them up with reasons, acting in accord with reasons and beliefs, drawing inferences from available evidence, and so on.

This reasoning activity can be done well and it can be done badly; it can be done correctly or incorrectly. Logic is the discipline that aims to distinguish good reasoning from bad.

Good reasoning is not necessarily effective reasoning. In fact, as we shall see in a subsequent chapter on logical fallacies, bad reasoning is pervasive and often extremely effective—in the sense that people are often persuaded by it. In logic, the standard of goodness is not effectiveness in the sense of persuasiveness, but rather correctness according to logical rules.

For example, consider Hitler. He persuaded an entire nation to go along with a variety of proposals that were not only false but downright evil. You won’t be surprised to hear that if you examine it critically, his reasoning does not pass logical muster. Hitler’s arguments were effective, but not logically correct. Moreover, his persuasive techniques go beyond reasoning in the sense of backing up claims with reasons. Hitler relied on threats, emotional manipulation, unsupported assertions, etc. There are many rhetorical tricks one can use to persuade.

In logic, we study the rules and techniques that allow us to distinguish good, correct reasoning from bad, incorrect reasoning.

Since there are a variety of different types of reasoning and methods with which to evaluate each of these types, plus various diverging views on what constitutes correct reasoning, there are many approaches to the logical enterprise. We talk of logic, but also of logics. A logic is just a set of rules and techniques for distinguishing good reasoning from bad. A logic must formulate precise standards for evaluating reasoning and develop methods for applying those standards to particular instances.

Basic Notions

Reasoning involves claims or statements—making them and backing them up with reasons, drawing out their consequences. Propositions are the things we claim, state, assert.

Propositions are the kinds of things that can be true or false. They are expressed by declarative sentences. We use such sentences to make all sorts of assertions, from routine matters of fact (“the Earth revolves around the Sun”), to grand metaphysical theses (“reality is an unchanging, featureless, unified Absolute”), to claims about morality (“it is wrong to eat meat”).

It is important to distinguish sentences in the declarative mood, which express propositions, from sentences in other moods, which do not. Interrogative sentences, for example, ask questions (“Is it raining?”), and imperative sentences issue commands (“Don’t drink kerosene.”). It makes no sense to ask whether these kinds of sentences express truths or falsehoods, so they do not express propositions.

We also distinguish propositions from the sentences that express them, because a single proposition can be expressed by different sentences. “It’s raining” and “es regnet” both express the proposition that it’s raining; one sentence does it in English, the other in German. Also, “John loves Mary” and “Mary is loved by John” both express the same proposition.

The fundamental unit of reasoning is the argument. In logic, by “argument” we don’t mean a disagreement, a shouting match; rather, we define the term precisely:

Argument = a set of propositions, one of which, the conclusion, is (supposed to be) supported by  the others, the premises.

If we’re reasoning by making claims and backing them up with reasons, then the claim that’s being backed up is the conclusion of an argument; the reasons given to support it are the argument’s premises. If we’re reasoning by drawing an inference from a set of statements, then the inference we draw is the conclusion of an argument, and the statements from which it’s drawn are the premises.

We include the parenthetical hedge—“supposed to be”—in the definition to make room for bad arguments. A bad argument, very roughly speaking, is one where the premises fail to support the conclusion; a good argument’s premises actually do support the conclusion.

Analysis of Arguments

The following passage expresses an argument:

So does this passage:

Again, the ultimate purpose of logic is to evaluate arguments—to distinguish the good from the bad. To do so requires distinctions, definitions, principles, and techniques that will be outlined in subsequent chapters. For now, we will focus on identifying and reconstructing arguments.

The first task is to explicate arguments—to state explicitly their premises and conclusions. A perspicuous way to do this is simply to list declarative sentences expressing the relevant propositions, with a line separating the premises from the conclusion, thus:

1. McDonald’s pays their workers very low wages.
2. The animals that provide McDonald’s meat are raised in deplorable conditions.
3. McDonald’s food is very unhealthy.
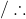4. You shouldn’t eat at McDonald’s. ^[1]

This is an explication of the first argumentative passage above. To identify the conclusion of an argument, it is helpful to ask oneself, “What is this person trying to convince me to believe by saying these things? What is the ultimate point of this passage?” The answer is pretty clear in this case. Another clue as to what’s going on in the passage is provided by the word “because” in the third sentence. Along with other words, like “since” and “for,” it indicates the presence of a premise. We can call such words premise markers. The symbol “/∴” can be read as shorthand for “therefore.” Along with expressions like “consequently,” “thus,” “it follows that” and “which implies that,” “therefore” is an indicator that the argument’s conclusion is about to follow. We call such locutions conclusion markers. Such a marker is not present in the first argument, but we do see one in the second, which may be explicated thus:

1. The universe is vast and complex.
2. The universe displays an astonishing degree of order.
3. The planets orbit the sun according to regular laws.
4. Animals’ minutest parts are arranged precisely to serve their purposes.
5. Such order and complexity cannot arise at random.
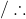6. The universe must be the product of a designer of enormous power and intellect: God.

Several points of comparison to our first explication are worthy of note here. First, as mentioned, we were alerted of the conclusion by the word “therefore.” Second, this passage required much more paraphrase than the first. The second sentence is interrogative, not declarative, and so it does not express a proposition. Since arguments are, by definition, collections of propositions, we must restrict ourselves to declarative sentences when explicating them. Since the answer to the second sentence’s rhetorical question is clearly “yes,” we paraphrase as shown. The third sentence expresses two propositions, so in our explication we separate them; each one is a premise.

So sometimes, when we explicate an argument, we have to take what’s present in the argumentative passage and change it slightly, so that all of the sentences we write down express the propositions present in the argument. This is paraphrasing. At other times, we have to do even more. For example, we may have to introduce propositions which are not explicitly mentioned within the argumentative passage, but are undoubtedly used within the argument’s reasoning.

There’s a Greek word for argumentative passages that leave certain propositions unstated: enthymemes. Here’s an example:

There’s an implicit premise lurking in the background here—something that hasn’t been said, but which needs to be true for the argument to go through. We need a claim that connects the premise to the conclusion—that bridges the gap between them. Something like this: An all-loving God would not allow innocent people to suffer. Or maybe: widespread suffering is incompatible with the idea of an all-loving deity. The premise points to suffering, while the conclusion is about God; these propositions connect those two claims. A complete explication of the argumentative passage would make a proposition like this explicit:

1. Many innocent people all over the world are suffering.
2. An all-loving God would not allow innocent people to suffer.
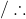3. There cannot be an all-loving God.

This is the mark of the kinds of tacit premises we want to uncover: if they’re false, they undermine the argument. Often, premises like this are unstated for a reason: they’re controversial claims on their own, requiring evidence to support them; so the arguer leaves them out, preferring not to get bogged down.^[2] When we draw them out, however, we can force a more robust dialectical exchange, focusing the argument on the heart of the matter. In this case, a discussion about the compatibility of God’s goodness and evil in the world would be in order. There’s a lot to be said on that topic. Philosophers and theologians have developed elaborate arguments over the centuries to defend the idea that God’s goodness and human suffering are in fact compatible.^[3]

So far, our analysis of arguments has not been particularly deep. We have noted the importance of identifying the conclusion and clearly stating the premises, but we have not looked into the ways in which sets of premises can support their conclusions. We have merely noted that, collectively, premises provide support for conclusions. We have not looked at how they do so, what kinds of relationships they have with one another. This requires deeper analysis.

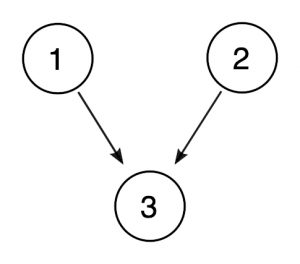
Often, different premises will support a conclusion—or another premise—individually, without help from any others. Consider this simple argument:

Propositions 1 and 2 support the conclusion, proposition 3—and they do so independently. Each gives us a reason for believing that the war was unjust, and each stands as a reason even if we were to suppose that the other were not true; this is the mark of independent premises.

It can be helpful, especially when arguments are more complex, to draw diagrams that depict the relationships among premises and conclusion. We could depict the argument above as follows:

In such a diagram, the circled numbers represent the propositions and the arrows represent the relationship of support from one proposition to another. Since propositions 1 and 2 each support 3 independently, they get their own arrows.

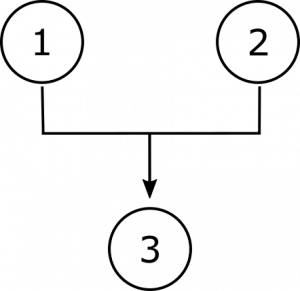
Other relationships among premises are possible. Sometimes, premises provide support for conclusions only indirectly, by giving us a reason to believe some other premise, which is intermediate between the two claims. Consider the following argument:

In this example, proposition 1 provides support for proposition 2 (the word “hence” is a clue), while proposition 2 directly supports the conclusion in 3. We would depict the relationships among these propositions thus:

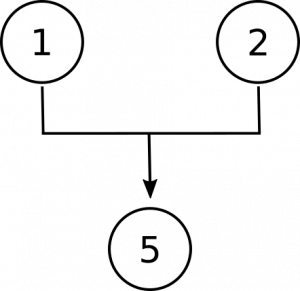
Sometimes premises must work together to provide support for another claim, not because one of them provides reason for believing the other, but because neither provides the support needed on its own; we call such propositions joint premises. Consider the following:

In this argument, neither premise 1 nor premise 2 supports the conclusion on its own; rather, the second premise, as it were, provides a key that unlocks the conclusion from the conditional premise 1. We can indicate such interdependence diagrammatically with brackets, thus:

Diagramming arguments in this way can be helpful both in understanding how they work and informing any attempt to critically engage with them. One can see clearly in the first argument that any considerations put forward contrary to one of the independent premises will not completely undermine support for the conclusion, as there is still another premise providing it with some degree of support. In the second argument, though, reasons telling against the second premise would cut off support for the conclusion at its root; and anything contrary to the first premise will leave the second in need of support. And in the third argument, considerations contrary to either of the joint premises will undermine support for the conclusion. Especially when arguments are more complex, such visual aids can help us recognize all of the inferences contained within the argument.

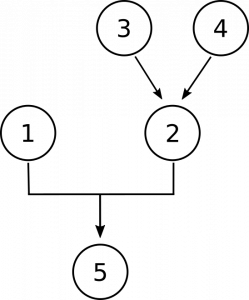
Perhaps it will be useful to conclude by considering a slightly more complex argument. Let’s consider the nature of numbers:

The conclusion of this argument is the last proposition, that numbers are abstract objects. Notice that the first premise gives us a choice between this claim and an alternative—that they are concrete. The second premise denies that alternative, and so premises 1 and 2 are working together to support the conclusion:

Now we need to make room in our diagram for propositions 3 and 4. They are there to give us reasons for believing that numbers are not concrete objects. First, by asserting that numbers aren’t located in space like concrete objects are, and second by asserting that numbers don’t interact with other objects, like concrete objects do. These are separate, independent reasons for believing they aren’t concrete, so we end up with this diagram:

Logic and Philosophy

At the heart of the logical enterprise is a philosophical question: What makes a good argument? That is, what is it for a set of claims to provide support for some other claim? Or maybe: When are we justified in drawing inferences? To answer these questions, logicians have developed a wide variety of logical systems, covering different types of arguments, and applying different principles and techniques. Many of the tools developed in logic can be applied beyond the confines of philosophy. The mathematician proving a theorem, the computer scientist programming a computer, the linguist modeling the structure of language—all these are using logical methods. Because logic has such wide application, and because of the formal/mathematical sophistication of many logical systems, it occupies a unique place in the philosophical curriculum. A class in logic is typically unlike other philosophy classes in that very little time is spent directly engaging with and attempting to answer the “big questions”; rather, one very quickly gets down to the business of learning logical formalisms. The questions logic is trying to answer are important philosophical questions, but the techniques developed to answer them are worthy of study on their own.

This does not mean, however, that we should think of logic and philosophy as merely tangentially related; on the contrary, they are deeply intertwined. For all the formal bells and whistles featured in the latest high-end logical system, at bottom it is part of an effort to answer the fundamental question of what follows from what. Moreover, logic is useful to the practicing philosopher in at least three other ways.

Philosophers attempt to answer deep, vexing questions—about the nature of reality, what constitutes a good life, how to create a just society, and so on. They give their answers to these questions, and they back those answers up with reasons. Then other philosophers consider their arguments and reply with elaborations and criticisms—arguments of their own. Philosophy is conducted and makes progress by way of exchanging arguments. Since they are the primary tool of their trade, philosophers better know a little something about what makes for good arguments! Logic, therefore, is essential to the practice of philosophy.

But logic is not merely a tool for evaluating philosophical arguments; it has altered the course of the ongoing philosophical conversation. As logicians developed formal systems to model the structure of an ever-wider range of discursive practices, philosophers have been able to apply their insights directly to traditional philosophical problems and recognize previously hidden avenues of inquiry. Since the turn of the 20th century especially, the proliferation of novel approaches in logic has sparked a revolution in the practice of philosophy. It is not too much of an exaggeration to say that much of the history of philosophy in the 20th century constituted an ongoing attempt to grapple with new developments in logic, and the philosophical focus on language that they seemed to demand. No philosophical topic—from metaphysics to ethics to epistemology and beyond—was untouched by this revolution.

Finally, logic itself is the source of fascinating philosophical questions. The basic question at its heart—what is it for a claim to follow from others?—ramifies out in myriad directions, providing fertile ground for philosophical speculation. There is logic, and then there is philosophy of logic. Logic is said to be “formal,” for example. What does that mean? It’s a surprisingly difficult question to answer.^[5] Our simplest logical formulations of conditional sentences (those involving “if”), lead to apparent paradoxes.^[6] How should those be resolved? Should our formalisms be altered to better capture the natural-language meanings of conditionals? What is the proper relationship between logical systems and natural languages, anyway?

Traditionally, most logicians have accepted that logic should be “bivalent”: every proposition is either true or false. But natural languages contain vague terms whose boundaries of applicability are not always clear. For example, “bald”: for certain subjects, we might be inclined to say that they’re well on their way to full-on baldness, but not quite there yet; on the other hand, we would be reluctant to say that they’re not-bald. There are in-between cases. For such cases, we might want to say, for example, that the proposition that Fredo is bald is neither true nor false. Some logicians have developed logics that are not bivalent, to deal with this sort of linguistic phenomenon. Some add a third truth-value: “neither” or “undetermined,” for instance. Others introduce infinite degrees of truth (this is called “fuzzy logic”). These logics deviate from traditional approaches. Are they therefore wrong in some sense? Or are they right, and the traditionalists wrong? Or are we even asking a sensible question when we ask whether a particular logical system is right or wrong? Can we be so-called logical “pluralists,” accepting a variety of incompatible logics, depending, for example, on whether they’re useful?

These sorts of questions are beyond the scope of this introductory text, of course. They’re included to give you a sense of just how far one can take the study of logic. The task for now, though, is to begin that study.